Why to use an intermediate representation
Intermediate representation of binary code is widely used in code analysis tools mostly by following reasons:
- Binary code is complicated. For example, IA-32 instruction set has more than one thousand of instructions, while OpenREIL has only 23. Obviously, it will be much more easy to write a program that analyzes IR code than machine or assembly code.
- Binary code has side effects. CPU instructions are usually doing an implicit operations like flags computation, also there's a lot of complex instructions that belongs to CISC or SIMD classes. For example, here is BAP IR representation of add rbx, rax x86 instruction, looks much more complex than original assembly instruction, right?
addr 0x0 @asm "add %rax,%rbx" label pc_0x0 T_t1:u64 = R_RBX:u64 T_t2:u64 = R_RAX:u64 R_RBX:u64 = R_RBX:u64 + T_t2:u64 R_CF:bool = R_RBX:u64 < T_t1:u64 R_OF:bool = high:bool((T_t1:u64 ^ ~T_t2:u64) & (T_t1:u64 ^ R_RBX:u64)) R_AF:bool = 0x10:u64 == (0x10:u64 & (R_RBX:u64 ^ T_t1:u64 ^ T_t2:u64)) R_PF:bool = ~low:bool(let T_acc:u64 := R_RBX:u64 >> 4:u64 ^ R_RBX:u64 in let T_acc:u64 := T_acc:u64 >> 2:u64 ^ T_acc:u64 in T_acc:u64 >> 1:u64 ^ T_acc:u64) R_SF:bool = high:bool(R_RBX:u64) R_ZF:bool = 0:u64 == R_RBX:u64 - There's a lot of different processor architectures at the market. Using of intermediate representation allows you to make your code analysis logic architecturally independent. Currently OpenREIL supports only i386 (please note that it's very early release ☺) but in a near future I'm planning to add x86_64 and ARM as well, it will be relatively easy because all these architectures are supported by VEX (a part of Valgrind which used in OpenREIL).
Kao's Toy Project
To demonstrate the power of OpenREIL let's solve Kao's Toy Project crackme. The following code is essence of this crackme, it's actually simple stream cipher with 64-bit key:
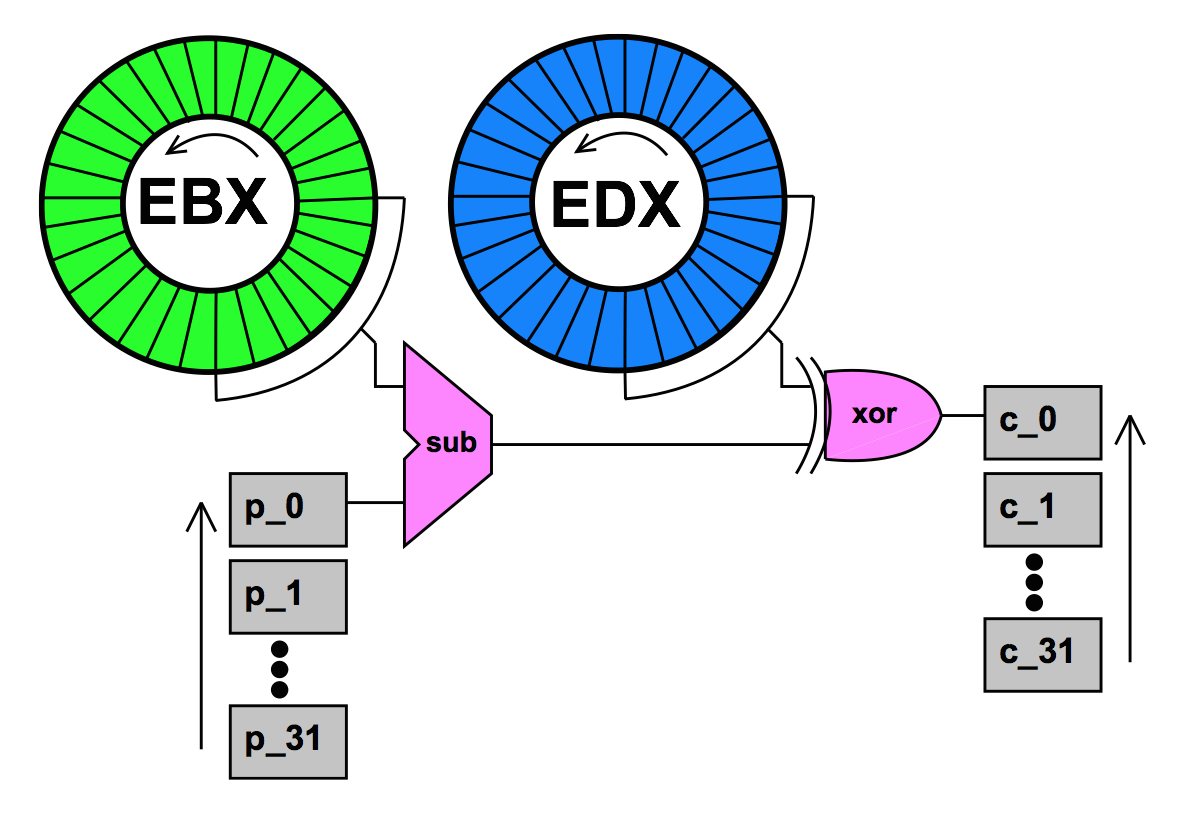
void expand(u8 out[32], const u8 in[32], u32 x, u32 y) { for (u32 i = 0; i < 32; ++i) { out[i] = (in[i] - x) ^ y; x = ROL(x, 1); y = ROL(y, 1); } }
It accepts 32-byte plain text as in, cipher key as x and y 32-bit unsigned integers, and produces 32-byte ciphered text out. Kao's Toy Project uses installation ID as plain text, serial number entered by user as x and y, and then compares encryption results with hardcoded ciphered text:
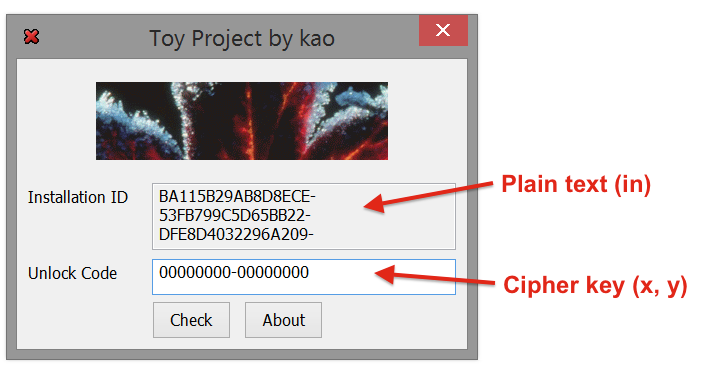
To solve the puzzle you need to recover encryption key for given function with the knowledge of plain text and ciphered text. The solution and cipher itself is not so simple as it could be at first look, paper that describes a solving of this puzzle was published by Dcoder in 2012 [PDF]:
First, try to solve the problem by hand a bit to develop a feel of the difficulty of the problem. For any single byte pair of plaintext and ciphertext (pi, ci) it’s quite easy to find 8 bits within the key so that the mapping is correct. In fact, you can choose ANY byte in EBX to subtract, since you can adjust the difference via the xor by the corresponding byte in EDX.
The value of the key for each byte mapping is completely open ended (256 possibilities). But actually choosing a value for the key for that mapping propagates a constraint across the possibilities of the other parts of the key. And this is the beauty of the algorithm.
Later after the publication Rolf Rolles released his own solution of this crackme, he used Satisfiability Modulo Theories (SMT) formula and SMT solver to achieve the solution. The formula does not explicitly take advantage of any aforementioned, known flaw in the cryptosystem, and instead encodes the algorithm literally. Symbolic execution was used to produce the formula automatically. Rolf also made a video demo with detailed explanation of all steps that needed to solve the puzzle (trace generation, trace simplification, SMT constraints generation and solving). Unfortunately Rolf didn't published the full code, but there's enough technical details to understand how his solution works.
Also, in 2013 Georgy Nosenko presented his work "SMT Solvers for Software Security" where BAP was used for Kao's Toy Project automated keygen generation. I believe, that it might be a good tradition among security reserachers to solve this nifty crackme for demonstrating applied use of some code analysis tools or frameworks ☺
Using OpenREIL for symbolic execution
Here is disassembled code of check_serial() function that checks entered key:
.text:004010EC check_serial proc near .text:004010EC .text:004010EC ciphered = byte ptr -21h .text:004010EC X = dword ptr 8 .text:004010EC Y = dword ptr 0Ch .text:004010EC .text:004010EC push ebp .text:004010ED mov ebp, esp .text:004010EF add esp, 0FFFFFFDCh .text:004010F2 mov ecx, 20h .text:004010F7 mov esi, offset installation_ID .text:004010FC lea edi, [ebp+text_ciphered] .text:004010FF mov edx, [ebp+X] .text:00401102 mov ebx, [ebp+Y] .text:00401105 .text:00401105 loc_401105: .text:00401105 lodsb .text:00401106 sub al, bl .text:00401108 xor al, dl .text:0040110A stosb .text:0040110B rol edx, 1 .text:0040110D rol ebx, 1 .text:0040110F loop loc_401105 .text:00401111 mov byte ptr [edi], 0 .text:00401114 push offset text_valid ; "0how4zdy81jpe5xfu92kar6cgiq3lst7" .text:00401119 lea eax, [ebp+text_ciphered] .text:0040111C push eax .text:0040111D call lstrcmpA .text:00401122 leave .text:00401123 retn 8 .text:00401123 check_serial endp
As you can see, it loads plain text pointer to ESI register at 004010F7 instruction, then instruction 004010FC loads pointer to stack buffer for ciphered text into the EDI register, encryption key entered by user is stored in EDX and EBX registers. Instructions from 00401105 to 0040110F runs 32 encryption cycles for each byte of input data. At the end of the function, at instruction 0040111D, strcmp() is being called to compare computed ciphered text with some reference value text_valid that hardcoded into the binary - entered encryption key is valid when they are equal.
We going to write a program that analyses Kao's binary and generates correct key for given installation ID mostly in the same way like it was done by Rolf. Here is a list of the steps that we need to do:
- Translate check_serial() function into REIL, apply some code optimizations to eliminate unused x86 flags computations, etc.
- Mark EDX and EBX registers as symbolic, initialize emulator memory with required global variables (text_valid, installation_ID) and run symbolic execution of our function. At the end of the symbolic execution text_ciphered buffer contents will be represented by 32 symbolic expressions (one for each byte) that accepts EDX and EBX variables as input arguments.
- Generate SMT constraints for achieved expressions by equating them with bytes of text_valid.
- Feed generated constraints to the SMT solver from Microsoft Z3 using z3py API, ask solver to check constraints satisfiability and produce valid input for EDX and EBX.

Let's do the first step with OpenREIL Python API:
from pyopenreil.REIL import * from pyopenreil.symbolic import * from pyopenreil.VM import * from pyopenreil.utils import bin_PE # VA's of required functions and variables check_serial = 0x004010EC installation_ID = 0x004093A8 # create translator instance tr = CodeStorageTranslator(bin_PE.Reader('toyproject.exe')) # construct data flow graph of check_serial() function dfg = DFGraphBuilder(tr).traverse(check_serial) # Run all available code optimizations and update # storage with new function code. dfg.optimize_all(tr.storage) # print generated IR code print tr.get_func(check_serial)
Generated IR code:
; sub_004010ec() ; Code chunks: 0x4010ec-0x401125 ; -------------------------------- ; ; asm: push ebp ; data (1): 55 ; 004010ec.00 SUB R_ESP:32, 4:32, R_ESP:32 004010ec.01 STM R_EBP:32, , R_ESP:32 ; ; asm: mov ebp, esp ; data (2): 8b ec ; 004010ed.00 STR R_ESP:32, , R_EBP:32 ; ; asm: add esp, -0x24 ; data (3): 83 c4 dc ; 004010ef.00 ADD R_ESP:32, ffffffdc:32, R_ESP:32 ; ; asm: mov ecx, 0x20 ; data (5): b9 20 00 00 00 ; 004010f2.00 STR 20:32, , R_ECX:32 ; ; asm: mov esi, 0x4093a8 ; data (5): be a8 93 40 00 ; 004010f7.00 STR 4093a8:32, , R_ESI:32 ; ; asm: lea edi, dword ptr [ebp + 0xffffffdf] ; data (3): 8d 7d df ; 004010fc.00 ADD R_EBP:32, ffffffdf:32, R_EDI:32 ; ; asm: mov edx, dword ptr [ebp + 8] ; data (3): 8b 55 08 ; 004010ff.00 ADD R_EBP:32, 8:32, V_01:32 004010ff.01 LDM V_01:32, , R_EDX:32 ; ; asm: mov ebx, dword ptr [ebp + 0xc] ; data (3): 8b 5d 0c ; 00401102.00 ADD R_EBP:32, c:32, V_01:32 00401102.01 LDM V_01:32, , R_EBX:32 ; ; asm: lodsb al, byte ptr [esi] ; data (1): ac ; 00401105.00 LDM R_ESI:32, , V_02:8 00401105.01 AND R_EAX:32, ffffff00:32, V_03:32 00401105.02 OR V_02:8, 0:8, V_04:32 00401105.03 OR V_03:32, V_04:32, R_EAX:32 00401105.04 ADD R_ESI:32, R_DFLAG:32, R_ESI:32 ; ; asm: sub al, bl ; data (2): 2a c3 ; 00401106.00 AND R_EAX:32, ff:32, V_00:8 00401106.01 AND R_EBX:32, ff:32, V_01:8 00401106.02 SUB V_00:8, V_01:8, V_02:8 00401106.03 AND R_EAX:32, ffffff00:32, V_05:32 00401106.04 OR V_02:8, 0:8, V_06:32 00401106.05 OR V_05:32, V_06:32, R_EAX:32 ; ; asm: xor al, dl ; data (2): 32 c2 ; 00401108.00 AND R_EAX:32, ff:32, V_00:8 00401108.01 AND R_EDX:32, ff:32, V_01:8 00401108.02 XOR V_00:8, V_01:8, V_02:8 00401108.03 AND R_EAX:32, ffffff00:32, V_04:32 00401108.04 OR V_02:8, 0:8, V_05:32 00401108.05 OR V_04:32, V_05:32, R_EAX:32 ; ; asm: stosb byte ptr es:[edi], al ; data (1): aa ; 0040110a.00 AND R_EAX:32, ff:32, V_01:8 0040110a.01 STM V_01:8, , R_EDI:32 0040110a.02 ADD R_EDI:32, R_DFLAG:32, R_EDI:32 ; ; asm: rol edx, 1 ; data (2): d1 c2 ; 0040110b.00 OR 1f:8, 0:8, V_01:32 0040110b.01 SHR R_EDX:32, V_01:32, V_02:32 0040110b.02 OR 1:8, 0:8, V_03:32 0040110b.03 SHL R_EDX:32, V_03:32, V_04:32 0040110b.04 OR V_04:32, V_02:32, R_EDX:32 ; ; asm: rol ebx, 1 ; data (2): d1 c3 ; 0040110d.00 OR 1f:8, 0:8, V_01:32 0040110d.01 SHR R_EBX:32, V_01:32, V_02:32 0040110d.02 OR 1:8, 0:8, V_03:32 0040110d.03 SHL R_EBX:32, V_03:32, V_04:32 0040110d.04 OR V_04:32, V_02:32, R_EBX:32 ; ; asm: loop -0xa ; data (2): e2 f4 ; 0040110f.00 SUB R_ECX:32, 1:32, R_ECX:32 0040110f.01 EQ R_ECX:32, 0:32, V_03:1 0040110f.02 NOT V_03:1, , V_02:1 0040110f.03 JCC V_02:1, , 401105:32 0040110f.04 JCC 1:1, , 401111:32 ; ; asm: mov byte ptr [edi], 0 ; data (3): c6 07 00 ; 00401111.00 STM 0:8, , R_EDI:32 ; ; asm: push 0x409185 ; data (5): 68 85 91 40 00 ; 00401114.00 SUB R_ESP:32, 4:32, R_ESP:32 00401114.01 STM 409185:32, , R_ESP:32 ; ; asm: lea eax, dword ptr [ebp + 0xffffffdf] ; data (3): 8d 45 df ; 00401119.00 ADD R_EBP:32, ffffffdf:32, R_EAX:32 ; ; asm: push eax ; data (1): 50 ; 0040111c.00 SUB R_ESP:32, 4:32, R_ESP:32 0040111c.01 STM R_EAX:32, , R_ESP:32 ; ; asm: call 0x1f1 ; data (5): e8 ec 01 00 00 ; 0040111d.00 SUB R_ESP:32, 4:32, R_ESP:32 0040111d.01 STM 401122:32, , R_ESP:32 0040111d.02 JCC 1:1, , 40130e:32 ; ; asm: leave ; data (1): c9 ; 00401122.00 STR R_EBP:32, , V_00:32 00401122.01 LDM V_00:32, , R_EBP:32 00401122.02 ADD V_00:32, 4:32, R_ESP:32 ; ; asm: ret 8 ; data (3): c2 08 00 ; 00401123.00 LDM R_ESP:32, , V_01:32 00401123.01 ADD R_ESP:32, c:32, R_ESP:32 00401123.02 JCC 1:1, , V_01:32
Unfortunately current version of OpenREIL still haven't symbolic execution implementation, but it provides API for constructing symbolic expressions and IR code emulation, which is enough to implement symbolic execution on the top of the pyopenreil.VM module with extending of VM.Math, VM.Mem, VM.Reg and VM.Cpu classes.
Normally, each register of VM.Cpu (which is represented by VM.Reg) keeps current value as Python long, but our new class that inherits VM.Reg uses Val object to store register value. It has two fields: Val.val and Val.exp, not None value of val indicates that it's a concrete value (just like a value of real CPU register), None value of val indicates that it's a symbolic value which expression is stored in exp.
Source code of these two classes:
class Val(object): def __init__(self, val = UNDEF, exp = None): self.val, self.exp = val, exp def __str__(self): return str(self.exp) if self.is_symbolic() else hex(self.val) def is_symbolic(self): # check if value is symbolic return self.val is None def is_concrete(self): # check if value is concrete return not self.is_symbolic() def to_z3(self, state, size): # # generate Z3 expression that represents this value # def _z3_size(size): return { U1: 1, U8: 8, U16: 16, U32: 32, U64: 64 }[ size ] def _z3_exp(exp, size): if isinstance(exp, SymVal): if state.has_key(exp.name): return state[exp.name] else: return z3.BitVec(exp.name, _z3_size(exp.size)) elif isinstance(exp, SymConst): return z3.BitVecVal(exp.val, _z3_size(exp.size)) elif isinstance(exp, SymExp): a, b = exp.a, exp.b assert isinstance(a, SymVal) or isinstance(a, SymConst) assert b is None or isinstance(b, SymVal) or isinstance(b, SymConst) assert b is None or a.size == b.size a = a if a is None else _z3_exp(a, a.size) b = b if b is None else _z3_exp(b, b.size) # makes 1 bit bitvectors from booleans _z3_bool_to_bv = lambda exp: z3.If(exp, z3.BitVecVal(1, 1), z3.BitVecVal(0, 1)) # z3 expression from SymExp ret = { I_ADD: lambda: a + b, I_SUB: lambda: a - b, I_NEG: lambda: -a, I_MUL: lambda: a * b, I_DIV: lambda: z3.UDiv(a, b), I_MOD: lambda: z3.URem(a, b), I_SHR: lambda: z3.LShR(a, b), I_SHL: lambda: a << b, I_OR: lambda: a | b, I_AND: lambda: a & b, I_XOR: lambda: a ^ b, I_NOT: lambda: ~a, I_EQ: lambda: _z3_bool_to_bv(a == b), I_LT: lambda: _z3_bool_to_bv(z3.ULT(a, b)) }[exp.op]() size_src = _z3_size(exp.a.size) size_dst = _z3_size(size) if size_src > size_dst: # convert to smaller value return z3.Extract(size_dst - 1, 0, ret) elif size_src < size_dst: # convert to bigger value return z3.Concat(z3.BitVecVal(0, size_dst - size_src), ret) else: return ret else: assert False if self.is_concrete(): # use concrete value return z3.BitVecVal(self.val, _z3_size(size)) else: # build Z3 expression return _z3_exp(self.exp, size) class Reg(VM.Reg): def to_symbolic(self): # get symbolic representation of register contents if self.val.is_concrete(): # use concrete value return SymConst(self.get_val(), self.size) else: if self.regs_map.has_key(self.name): return SymVal(self.regs_map[self.name], self.size) # use symbolic value return SymVal(self.name, self.size) if self.val.exp is None \ else self.val.exp def get_val(self): # get concrete value of the register if it's available assert self.val.is_concrete() return super(Reg, self).get_val(self.val.val) def str_val(self): return str(self.val.exp) if self.val.is_symbolic() \ else super(Reg, self).str_val(self.val.val)
Example of concrete value initialization:
val = Val(0x1337L)
Example of symbolic value initialization:
val = Val(exp = SymVal('R_EAX', U32) + SymConst(1L, U32))
Engine computes concrete values during IR instructions execution always when it's possible, but when it meets any instruction that accepts a symbolic value as input - result of it's execution will be a symbolic. Handling of most of the IR instructions is implemented in VM.Math class, here is the source code of inherited symbolic class for it:
class Math(VM.Math): def eval(self, op, a = None, b = None): concrete = True a_val = a if a is None else a.val b_val = b if b is None else b.val # determinate symbolic/concrete operation mode if a_val is not None and a_val.is_symbolic(): concrete = False if b_val is not None and b_val.is_symbolic(): concrete = False if concrete: a_reg = a if a is None else VM.Reg(a.size, a.get_val()) b_reg = b if b is None else VM.Reg(b.size, b.get_val()) # compute and return concrete value return Val(val = super(Math, self).eval(op, a_reg, b_reg)) else: assert a is not None assert op in [ I_STR, I_NOT ] or b is not None # get symbolic representation of the arguments a_sym = a if a is None else a.to_symbolic() b_sym = b if b is None else b.to_symbolic() # make a symbolic expression exp = a_sym if op == I_STR else SymExp(op, a_sym, b_sym) # return symbolic value return Val(exp = exp)
Symbolic version of VM.Mem class is also uses Val objects to represent each byte of emulator's memory. Currently my symbolic memory model is far away from perfect, but in the case of Kao's crackme it's good enough to track values and expressions across the memory reads-writes. Symbolic version of VM.Cpu collects all register value assignments in SSA form and saves them to list that available as VM.Cpu.regs_list field. Here is execution trace of check_serial():
R_EIP_0_0_0 = 0x0 R_DFLAG_0_0_0 = 0x1 R_EAX_0_0_0 = 0x0 R_EBP_0_0_0 = 0x42424242 R_ESP_0_0_0 = 0x12000ff4 R_EIP_0_0_1 = 0x4010ec R_ESP_4010ec_0_0 = 0x12000ff0L R_EIP_4010ec_0_0 = 0x4010ecL R_EIP_4010ec_1_0 = 0x4010edL R_EBP_4010ed_0_0 = 0x12000ff0L R_EIP_4010ed_0_0 = 0x4010efL R_ESP_4010ef_0_0 = 0x12000fccL R_EIP_4010ef_0_0 = 0x4010f2L R_ECX_4010f2_0_0 = 0x20L R_EIP_4010f2_0_0 = 0x4010f7L R_ESI_4010f7_0_0 = 0x4093a8L R_EIP_4010f7_0_0 = 0x4010fcL R_EDI_4010fc_0_0 = 0x12000fcfL R_EIP_4010fc_0_0 = 0x4010ffL V_01_4010ff_0_0 = 0x12000ff8L R_EIP_4010ff_0_0 = 0x4010ffL R_EDX_4010ff_1_0 = ONE R_EIP_4010ff_1_0 = 0x401102L V_01_401102_0_0 = 0x12000ffcL R_EIP_401102_0_0 = 0x401102L R_EBX_401102_1_0 = TWO R_EIP_401102_1_0 = 0x401105L V_02_401105_0_0 = 0x0 R_EIP_401105_0_0 = 0x401105L V_03_401105_1_0 = 0x0L R_EIP_401105_1_0 = 0x401105L V_04_401105_2_0 = 0x0L R_EIP_401105_2_0 = 0x401105L R_EAX_401105_3_0 = 0x0L R_EIP_401105_3_0 = 0x401105L R_ESI_401105_4_0 = 0x4093a9L R_EIP_401105_4_0 = 0x401106L V_00_401106_0_0 = 0x0L R_EIP_401106_0_0 = 0x401106L V_01_401106_1_0 = (R_EBX_401102_1_0 & 0xff) R_EIP_401106_1_0 = 0x401106L V_02_401106_2_0 = (0x0 - V_01_401106_1_0) R_EIP_401106_2_0 = 0x401106L V_05_401106_3_0 = 0x0L R_EIP_401106_3_0 = 0x401106L V_06_401106_4_0 = (V_02_401106_2_0 | 0x0) R_EIP_401106_4_0 = 0x401106L R_EAX_401106_5_0 = (0x0 | V_06_401106_4_0) R_EIP_401106_5_0 = 0x401108L V_00_401108_0_0 = (R_EAX_401106_5_0 & 0xff) R_EIP_401108_0_0 = 0x401108L V_01_401108_1_0 = (R_EDX_4010ff_1_0 & 0xff) R_EIP_401108_1_0 = 0x401108L V_02_401108_2_0 = (V_00_401108_0_0 ^ V_01_401108_1_0) R_EIP_401108_2_0 = 0x401108L V_04_401108_3_0 = (R_EAX_401106_5_0 & 0xffffff00) R_EIP_401108_3_0 = 0x401108L V_05_401108_4_0 = (V_02_401108_2_0 | 0x0) R_EIP_401108_4_0 = 0x401108L R_EAX_401108_5_0 = (V_04_401108_3_0 | V_05_401108_4_0) R_EIP_401108_5_0 = 0x40110aL V_01_40110a_0_0 = (R_EAX_401108_5_0 & 0xff) R_EIP_40110a_0_0 = 0x40110aL R_EIP_40110a_1_0 = 0x40110aL R_EDI_40110a_2_0 = 0x12000fd0L R_EIP_40110a_2_0 = 0x40110bL V_01_40110b_0_0 = 0x1fL R_EIP_40110b_0_0 = 0x40110bL V_02_40110b_1_0 = (R_EDX_4010ff_1_0 >> 0x1f) R_EIP_40110b_1_0 = 0x40110bL V_03_40110b_2_0 = 0x1L R_EIP_40110b_2_0 = 0x40110bL V_04_40110b_3_0 = (R_EDX_4010ff_1_0 << 0x1) R_EIP_40110b_3_0 = 0x40110bL R_EDX_40110b_4_0 = (V_04_40110b_3_0 | V_02_40110b_1_0) R_EIP_40110b_4_0 = 0x40110dL V_01_40110d_0_0 = 0x1fL R_EIP_40110d_0_0 = 0x40110dL V_02_40110d_1_0 = (R_EBX_401102_1_0 >> 0x1f) R_EIP_40110d_1_0 = 0x40110dL V_03_40110d_2_0 = 0x1L R_EIP_40110d_2_0 = 0x40110dL V_04_40110d_3_0 = (R_EBX_401102_1_0 << 0x1) R_EIP_40110d_3_0 = 0x40110dL R_EBX_40110d_4_0 = (V_04_40110d_3_0 | V_02_40110d_1_0) R_EIP_40110d_4_0 = 0x40110fL R_ECX_40110f_0_0 = 0x1fL R_EIP_40110f_0_0 = 0x40110fL V_03_40110f_1_0 = 0x0 R_EIP_40110f_1_0 = 0x40110fL V_02_40110f_2_0 = 0x1 R_EIP_40110f_2_0 = 0x40110fL V_02_401105_0_1 = 0x1 R_EIP_401105_0_1 = 0x401105L V_03_401105_1_1 = (R_EAX_401108_5_0 & 0xffffff00) R_EIP_401105_1_1 = 0x401105L V_04_401105_2_1 = 0x1L R_EIP_401105_2_1 = 0x401105L R_EAX_401105_3_1 = (V_03_401105_1_1 | 0x1) R_EIP_401105_3_1 = 0x401105L R_ESI_401105_4_1 = 0x4093aaL R_EIP_401105_4_1 = 0x401106L V_00_401106_0_1 = (R_EAX_401105_3_1 & 0xff) R_EIP_401106_0_1 = 0x401106L V_01_401106_1_1 = (R_EBX_40110d_4_0 & 0xff) R_EIP_401106_1_1 = 0x401106L V_02_401106_2_1 = (V_00_401106_0_1 - V_01_401106_1_1) R_EIP_401106_2_1 = 0x401106L V_05_401106_3_1 = (R_EAX_401105_3_1 & 0xffffff00) R_EIP_401106_3_1 = 0x401106L V_06_401106_4_1 = (V_02_401106_2_1 | 0x0) R_EIP_401106_4_1 = 0x401106L R_EAX_401106_5_1 = (V_05_401106_3_1 | V_06_401106_4_1) R_EIP_401106_5_1 = 0x401108L V_00_401108_0_1 = (R_EAX_401106_5_1 & 0xff) R_EIP_401108_0_1 = 0x401108L V_01_401108_1_1 = (R_EDX_40110b_4_0 & 0xff) R_EIP_401108_1_1 = 0x401108L V_02_401108_2_1 = (V_00_401108_0_1 ^ V_01_401108_1_1) R_EIP_401108_2_1 = 0x401108L V_04_401108_3_1 = (R_EAX_401106_5_1 & 0xffffff00) R_EIP_401108_3_1 = 0x401108L V_05_401108_4_1 = (V_02_401108_2_1 | 0x0) R_EIP_401108_4_1 = 0x401108L R_EAX_401108_5_1 = (V_04_401108_3_1 | V_05_401108_4_1) R_EIP_401108_5_1 = 0x40110aL V_01_40110a_0_1 = (R_EAX_401108_5_1 & 0xff) R_EIP_40110a_0_1 = 0x40110aL R_EIP_40110a_1_1 = 0x40110aL R_EDI_40110a_2_1 = 0x12000fd1L R_EIP_40110a_2_1 = 0x40110bL V_01_40110b_0_1 = 0x1fL R_EIP_40110b_0_1 = 0x40110bL V_02_40110b_1_1 = (R_EDX_40110b_4_0 >> 0x1f) R_EIP_40110b_1_1 = 0x40110bL V_03_40110b_2_1 = 0x1L R_EIP_40110b_2_1 = 0x40110bL V_04_40110b_3_1 = (R_EDX_40110b_4_0 << 0x1) R_EIP_40110b_3_1 = 0x40110bL R_EDX_40110b_4_1 = (V_04_40110b_3_1 | V_02_40110b_1_1) ... around 2000 of other items that was skipped, full trace is here
Symbolic CPU class also has to_z3() method that returns representation of the trace as list of Z3 bit vector expressions.
Now let's write a main function code that connects all of the pieces altogether:
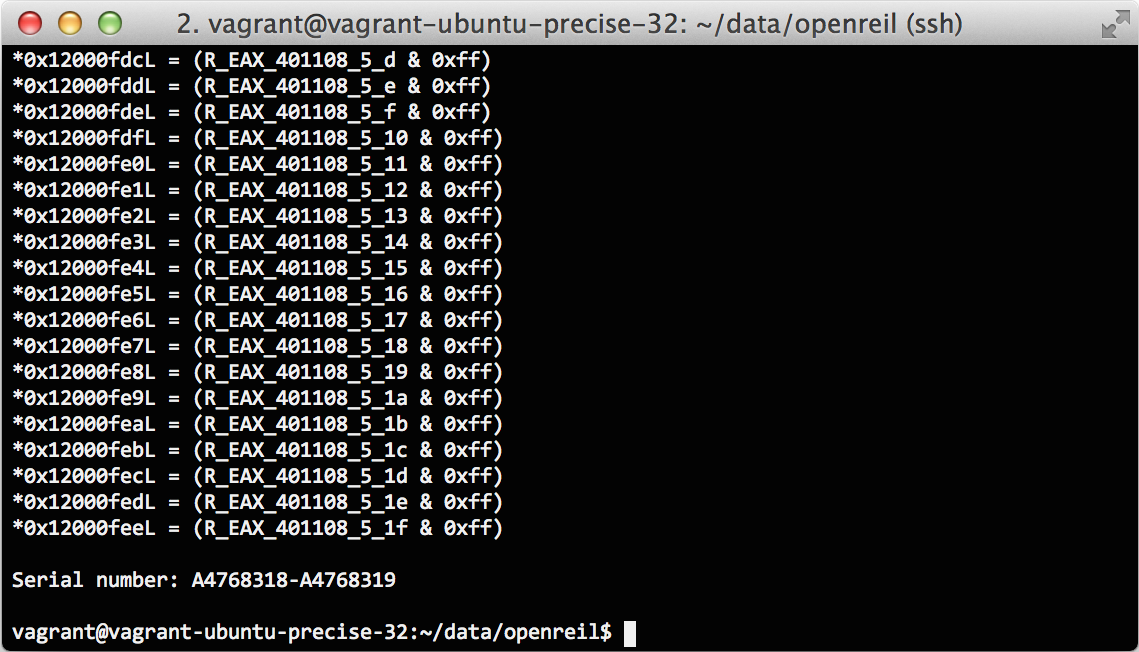
def keygen(kao_binary_path, kao_installation_ID): # address of the check_serial() function check_serial = 0x004010EC # address of the strcmp() call inside check_serial() stop_at = 0x0040111D # address of the global buffer with installation ID installation_ID = 0x004093A8 # load Kao's PE binary from pyopenreil.utils import bin_PE tr = CodeStorageTranslator(bin_PE.Reader(kao_binary_path)) # Construct DFG, run all available code optimizations # and update storage with new function code. dfg = DFGraphBuilder(tr).traverse(check_serial) dfg.optimize_all(tr.storage) print tr.get_func(check_serial) # create CPU and ABI cpu = Cpu(ARCH_X86) abi = VM.Abi(cpu, tr, no_reset = True) # hardcoded ciphered text constant from Kao's binary out_data = '0how4zdy81jpe5xfu92kar6cgiq3lst7' in_data = '' try: # convert installation ID into the binary form for s in kao_installation_ID.split('-'): in_data += struct.pack('L', int(s[:8], 16)) in_data += struct.pack('L', int(s[8:], 16)) assert len(in_data) == 32 except: raise Exception('Invalid instllation ID string') # copy installation ID into the emulator's memory for i in range(32): cpu.mem.store(installation_ID + i, U8, cpu.mem._Val(U8, 0, ord(in_data[i]))) ret, ebp = 0x41414141, 0x42424242 # create stack with symbolic arguments for check_serial() stack = abi.pushargs(( Val(exp = SymVal('ARG_0', U32)), \ Val(exp = SymVal('ARG_1', U32)) )) # dummy return address stack.push(Val(ret)) # initialize emulator's registers cpu.reg('ebp', Val(ebp)) cpu.reg('esp', Val(stack.top)) # run until stop try: cpu.run(tr, check_serial, stop_at = [ stop_at ]) except VM.CpuStop as e: print 'STOP at', hex(cpu.reg('eip').get_val()) # get Z3 expressions list for current CPU state state = cpu.to_z3() cpu.dump(show_all = True) # read symbolic expressions for contents of the output buffer addr = cpu.reg('eax').val data = cpu.mem.read(addr.val, 32) for i in range(32): print '*' + hex(addr.val + i), '=', data[i].exp # create SMT solver solver = z3.Solver() for i in range(32): # add constraint for each output byte solver.add(data[i].to_z3(state, U8) == z3.BitVecVal(ord(out_data[i]), 8)) # solve constraints solver.check() # get solution model = solver.model() # get and print serial number serial = map(lambda d: model[d].as_long(), model.decls()) serial[1] = serial[0] ^ serial[1] print '\nSerial number: %s\n' % '-'.join([ '%.8X' % serial[0], '%.8X' % serial[1] ]) return serial assert False
My quick and dirty symbolic execution engine isn't perfect, it has certain limitations that makes it unusable for any complex applications: incomplete memory model, very simple symbolic CPU that doesn't support such things like memory writes and jumps with symbolic address, jumps with symbolic condition, etc. Currently I included it into OpenREIL source code tree only as unit test and stand alone test application, but I'm planning to make a proper symbolic execution implementation and API for pyopenreil as well.
To use this keygen you need to build OpenREIL from Git repository, install Microsoft Z3 with Python bindings and run tests/test_kao.py program with your Kao's installation ID as argument:
$ python tests/test_kao.py 97FF58287E87FB74-979950C854E3E8B3-55A3F121A5590339-6A8DF5ABA981F7CE
And win!
It took around one second to perform all of the computations, which is very good.
Curious reader probably will ask me, is it possible to crack any much or less strong crypto algorithm from real world (like AES, for example ☺) in this way? Unfortunately no, SMT solvers are not magic artefacts and they can't curve laws of mathematics.